Latar Belakang Masalah
Urutan bilangan tripel Phytagoras sangat menarik untuk diperhatikan. Untuk mendapatkan bilangan tripel Phytagoras tidaklah terlalu sukar, karena secara baku dalam buku-buku ajar Matematika tingkat SLTP diberikan rumusnya. Namun ternyata rumusan itu tidak dapat difahami secara sederhana bagi sebagian besar siswa. Sehingga banyak siswa yang merasa bingung. Terutama dalam proses menghitung bilangan-bilangan untuk mendapatkan bilangan tripel Phytagoras dari dua bilangan asli yang secara bebas ditentukan.
Bertitik tolak dari kondisi tersebut mendorong penulis untuk melakukan modifikasi terhadap rumusan tripel Phytagoras melalui analisis matematis. Sehingga diharapkan akan didapat bentuk sederhana yang dapat dipertanggungjawabkan secara keilmuan.
Menyederhanakan Rumus Tripel Phytagoras
Tripel Phytagoras ( pada umumnya ) adalah susunan tiga buah bilangan asli yang memenuhi aturan Phytagoras. Jika bilangan-bilangan tersebut dinyatakan sebagai a, b dan c dengan a dan b adalah sisi-sisi siku-siku dan c adalah sisi miring ( hipotenusa ), maka akan berlaku :
c2 = a2 + b2
…………… ( 1 )
dimana:
a = 2mn …………... ( 2 )
b =
m2 – n2 .………….. ( 3 )
c = m2 + n2 …….…….. ( 4 )
m, n adalah bilangan-bilangan asli sembarang dan berbeda.
Terlihat bahwa untuk mendapatkan bilangan tripel Phytagoras terlebih dulu harus menentukan dua bilangan. Itu hal yang mudah, tapi tidak sederhana! Untuk membuat rumus diatas menjadi lebih sederhana maka diambil asumsi-asumsi sebagai berikut:
a < b < c …………… ( 5 )
Sehingga urutan bilangan tersebut dari yang terkecil adalah : a, b, c. Dengan mensubstitusikan persamaan-persamaan ( 2 ), ( 3 ), ( 4 ) ke pertidaksamaan ( 5 ), maka didapat bentuk:
2mn < m2 – n2 < m2 + n2
.....………... ( 6 )
Tanpa perlu pembuktian, sudah jelas bahwa: : m2 – n2 < m2 + n2
Akan dibuktikan bahwa:
2mn < m2 + n2
2mn < m2 + n2
dimana m ≠ n, atau:
m2 + n2 > 2mn
m2 + n2 – 2mn > 0
( m – n )2 > 0 ; kuadrat suatu bilangan selalu positif. ( Terbukti )
m2 + n2 > 2mn
m2 + n2 – 2mn > 0
( m – n )2 > 0 ; kuadrat suatu bilangan selalu positif. ( Terbukti )
Sekarang akan dibuktikan dengan syarat tertentu bahwa:
m2 – n2 > 2mn ……………
( 7 )
( m2 – n2 ) – 2mn > 0 …………… ( 8 )
Jika diambil:
β = ( m2 – n2 ) – 2mn …………… ( 9 )
Dengan membandingkan pertidaksamaan ( 8 ) dengan persamaan ( 9 ), maka terlihat bahwa β adalah bilangan positif. Sekarang ambil:
( m + n )2 = m2 + n2 + 2mn …………... ( 10 )
Tambahkan m2 – n2 pada kedua ruas dari persamaan ( 10 ), sehingga didapat:
m2 – n2 + ( m + n )2 = m2 – n2 + m2 + n2 + 2mn
m2 – n2 + ( m + n )2 = 2 m2 + 2mn
( m2 – n2 ) – 2mn = 2 m2 - ( m + n )2 ……………. ( 11 )
Terlihat bahwa bagian sebelah kiri dari persamaan ( 11 ) adalah menyatakan β. Sehingga persamaan ( 9 ) dapat berbentuk:
β = 2 m2 - ( m + n )2
…………… ( 12 )
β = ( m√2
+ m + n )( m√2 – m
– n ) …………… ( 13 )
Pada persamaan ( 13 ) karena m dan n adalah bilangan asli yang berbeda maka besaran: ( m√2 + m + n ) berharga positif, sehingga agar β bernilai positif, maka harus dipenuhi kondisi:
( m√2 – m – n ) > 0
( √2 – 1 )m – n > 0
Pertidaksamaan ( 14 ) adalah syarat agar pertidaksamaan ( 5 ) terpenuhi.
Rumusan yang Sederhana itu
Sebagaimana diketahui bahwa bilangan pertama suatu urutan tripel Phytagoras dapat berupa bilangan genap maupun bilangan ganjil. Sehingga untuk mendapatkan rumus urutan tripel Phytagoraspun diperlukan dua analisis, yaitu analisis dalam menentukan urutan tripel Phytagoras dengan bilangan pertama tripel adalah bilangan genap dan bilangan pertama tripel adalah bilangan ganjil.
1. Menentukan Urutan Tripel Phytagoras dengan Bilangan Pertama Tripel adalah Bilangan Genap
Jika sisi-sisi segitiga siku-siku pada persamaan-persamaan ( 2 ), ( 3 ) dan ( 4 ) dinyatakan dalam bentuk perbandingan antar sisi-sisi, maka didapat bentuk
a : b : c = 2mn : m2 – n2 : m2 + n2 …………… ( 16 )
diperoleh bentuk:
…………… ( 17 )
a : b : c = 2k : k2 – 1 : k2 + 1 ……………. ( 18 )
Dari persamaan ( 18 ) terlihat bahwa:
a = 2k ; k adalah bilangan asli …………….. ( 19 )
Sehingga a adalah adalah bilangan genap ( G ), maka persamaan ( 19 ) dapat ditulis:
……………. ( 20 )
Jika nilai k pada persamaan ( 20 ) disubstitusikan pada persamaan 18, maka didapat bentuk:
…………… ( 21 )
Persamaan ( 21 ) menyatakan bilangan dasar dari tripel Phytagoras, sehingga nilai-nilai dari a, b dan c adalah sebagai berikut:
…………… ( 23 )
…………… ( 24 )
Dari persamaan-persamaan ( 23 ) dan ( 24 ) didapat dua hubungan yang penting, yaitu:
…………… ( 26 )
2. Menentukan Urutan Tripel Phytagoras dengan Bilangan Pertama Tripel adalah Bilangan Ganjil
Dengan membagi ruas kanan persamaan ( 16 ) dengan 2n2 maka akan diperoleh bentuk sebagai berikut:
……………. ( 27 )
Berdasarkan persamaan ( 15 )  adalah bilangan ganjil, maka
adalah bilangan ganjil, maka  adalah bilangan asli. Jika diinginkan bahwa
adalah bilangan asli. Jika diinginkan bahwa  harus dinyatakan dalam bentuk
harus dinyatakan dalam bentuk
Dengan mensubstitusikan persamaan ( 28 ) ke persamaan ( 27 ), maka didapat
bentuk:
karena 2k + 1 menyatakan bilangan ganjil untuk setiap k bilangan asli, maka:
'
………….. ( 30 )
Dengan mensubstitusikan persamaan ( 30 ) ke persamaan ( 29 ), maka akan didapat bentuk sebagai berikut:
Persamaan ( 31 ) menyatakan bilangan dasar dari tripel Phytagoras, sehingga nilai-nilai dari a, b dan c adalah sebagai berikut:
…………. ( 33 )
…………. ( 34 )
Dari persamaan-persamaan ( 33 ) dan ( 34 ) didapat dua hubungan yang penting, yaitu:
Contoh Penggunaan Tripel Phytagoras
Kesimpulan
Dengan menetukan sembarang bilangan asli sebagai bilangan pertama bagi tripel









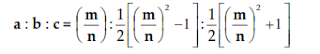











Berkomentar u/ kritik & saran yg baik, demi kemajuan bersama,,